Lingkaran atau bisa disebut sebagai segi-tak hingga dalam bidang geometri. Dalam bidang kartesius, lingkaran adalah titik-titik yang berjumlah tak hingga yang memiliki jarak yang sama dengan pusat lingkaran. Jarak dari setiap titik ke titik pusat biasa disebut sebagai jari-jari r.

Belajar persamaan lingkaran materi matematika kelas 11 SMA dengan contoh soal dan pembahasan.

Artikel awal ini membahas persamaan lingkaran dengan pusat titik (0, 0), titik (a, b) dan bentuk umum persamaan lingkaran, garis singgung pada lingkaran dibahas pada artikel tersendiri.

Soal No. 1
Berikut lukisan sebuah lingkaran pada sumbu x dan sumbu y.

Tentukan:
a) koordinat titik pusat lingkaran
b) jari-jari lingkaran
c) persamaan lingkaran

Pembahasan
a) koordinat titik pusat lingkaran
dari gambar terlihat bahwa koordinat pusat lingkaran adalah (0, 0)

b) jari-jari lingkaran
Jari-jari lingkaran r = 5

c) persamaan lingkaran
lingkaran dengan pusat titik (0, 0) dengan jari-jari r akan memiliki persamaan dengan bentuk :
x² + y² = r²



sehingga
x² + y² = 5²
x² + y² = 25

Soal No. 2
Suatu lingkaran memiliki persamaan:
x² + y² = 144

Tentukan panjang diameter lingkaran tersebut!

Pembahasan
Lingkaran pusat di (0, 0) di atas memiliki jari-jari:
r = √144
= 12 cm.

Diameter lingkaran:
D = 2 r
= 24 cm.

Soal No. 3
Diberikan sebuah lingkaran seperti gambar berikut!



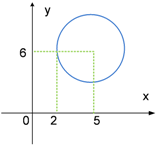
Tentukan:
a) koordinat titik pusat lingkaran
b) jari-jari lingkaran
c) persamaan lingkaran

Pembahasan
a) koordinat titik pusat lingkaran
pusat lingkaran terletak pada x = 5 dengan y = 6 sehingga koordinatnya adalah (5, 6)

b) jari-jari lingkaran
sesuai gambar diatas, jari-jari lingkaran adalah 5 − 2 = 3

c) persamaan lingkaran
lingkaran dengan titik pusat di (a, b) dengan jari-jari r akan memiliki persamaan berikut:
(x − a)² + (y − b)² = r²



dimana a = 5, dan b = 6
sehingga
(x − 5)² + (y − 6)² = 3²
(x − 5)² + (y − 6)² = 9

Soal No. 4
Persamaan suatu lingkaran adalah x² + y² − 8x + 4y − 5 = 0
Tentukan:
a) titik pusat lingkaran
b) jari-jari lingkaran

Pembahasan
Suatu lingkaran x² + y² + Ax + By + C = 0




akan memiliki titik pusat (−¹/₂A, −¹/₂ B) dan jari-jari r = √[¹/₄ A² + ¹/₄ B² −C] .

Dari persamaan lingkaran diatas nilai :
A = −8, B = 4 dan C = − 5

a) titik pusat (−¹/₂[−8], −¹/₂ [4]) = (4, −2)
b) jari-jari lingkaran r = √[¹/₄ (−8)² + ¹/₄ (4)² −(−5)] = √25 = 5